重复复制数组元素：在MATLAB中进行游程解码


Repeat copies of array elements: Run-length decoding in MATLAB

我正在尝试使用"值"数组和"计数器"数组将多个值插入到数组中。 例如，如果：

1
2
a=[1,3,2,5]
b=[2,2,1,3]

我想要一些功能的输出

1
c=somefunction(a,b)

成为

1
c=[1,1,3,3,2,5,5,5]

其中a(1)重复b(1)次，a(2)重复b(2)次，依此类推...

MATLAB中是否有内置函数可以执行此操作？ 如果可能，我想避免使用for循环。 我尝试了'repmat()'和'kron()'的变体，但无济于事。

这基本上是Run-length encoding。

基准测试

已针对R2015b更新：repelem现在对于所有数据大小都最快。

经过测试的功能：

  • R2015a中添加的MATLAB内置repelem函数
  • gnovice的cumsum解决方案(rld_cumsum)
  • Divakar的cumsum + diff解决方案(rld_cumsum_diff)
  • 这篇文章中knedlsepp的accumarray解决方案(knedlsepp5cumsumaccumarray)
  • 基于朴素循环的实现(naive_jit_test.m)测试即时编译器

    • R2015b上test_rld.m的结果：

    repelem time

    使用R2015a的旧时序图。

    发现：

    • repelem总是最快的两倍。
    • rld_cumsum_diff始终比rld_cumsum快。
    • repelem对于较小的数据大小(少于约300-500个元素)最快。
    • rld_cumsum_diff大约比repelem快约5000个元素
    • repelem在30000到300000个元素之间变得比rld_cumsum慢
    • rld_cumsum具有与knedlsepp5cumsumaccumarray大致相同的性能
    • naive_jit_test.m具有几乎恒定的速度，对于较小的尺寸，它与rld_cumsum和knedlsepp5cumsumaccumarray相同，对于较大的尺寸，则要快一些

    enter image description here

    使用R2015a的旧费率图。

    结论

    在大约5000个元素以下使用repelem ，在上面使用cumsum + diff解决方案。

    相关讨论

    问题陈述

    我们有一个值数组vals和游程长度runlens：

    1
    2
    vals     = [1,3,2,5]
    runlens  = [2,2,1,3]

    我们需要将vals中的每个元素重复runlens中的每个对应元素。因此，最终输出将是：

    1
    output = [1,1,3,3,2,5,5,5]

    前瞻性方法

    使用MATLAB最快的工具之一是cumsum，在处理对不规则模式起作用的矢量化问题时非常有用。在陈述的问题中，runlens中的不同元素带有不规则性。

    现在，要利用cumsum，我们需要在这里做两件事：初始化zeros的数组，并将"适当"的值放置在zeros数组的"键"位置，例如在应用" cumsum"之后，我们将最终得到重复的vals次(x1>次)的最终数组。

    步骤：让我们对上述步骤进行编号，以使预期方法更容易理解：

    1)初始化零数组：长度必须是多少？因为我们要重复runlens次，所以零数组的长度必须是所有runlens的总和。

    2)查找关键位置/索引：现在这些关键位置是沿着Zeros数组的位置，vals中的每个元素都将开始重复。
    因此，对于runlens = [2,2,1,3]，映射到zeros数组的键位置将是：

    1
    [X 0 X 0 X X 0 0] % where X's are those key positions.

    3)找到合适的值：在使用cumsum之前要锤打的最终钉子是将"合适的"值放入这些关键位置。现在，由于不久之后我们将开始使用cumsum，因此如果您仔细考虑，您将需要values的values版本和diff，这样在这些上的cumsum就会带回我们的values。由于将这些微分值放置在零点数组上，这些零点数组之间的距离为runlens，因此在使用cumsum之后，我们将每个vals元素重复runlens次作为最终输出。

    解决方案代码

    这是将上述所有步骤组合在一起的实现-

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    % Calculate cumsumed values of runLengths.
    % We would need this to initialize zeros array and find key positions later on.
    clens = cumsum(runlens)

    % Initalize zeros array
    array = zeros(1,(clens(end)))

    % Find key positions/indices
    key_pos = [1 clens(1:end-1)+1]

    % Find appropriate values
    app_vals = diff([0 vals])

    % Map app_values at key_pos on array
    array(pos) = app_vals

    % cumsum array for final output
    output = cumsum(array)

    预分配黑客

    可以看出，上面列出的代码使用带有零的预分配。现在，根据UNDOCUMENTED MATLAB关于更快的预分配的博客，使用以下命令可以实现更快的预分配：

    1
    array(clens(end)) = 0; % instead of array = zeros(1,(clens(end)))

    总结：功能代码

    要包装所有内容，我们将有一个紧凑的功能代码来实现这种游程长度解码，如下所示：

    1
    2
    3
    4
    5
    6
    function out = rle_cumsum_diff(vals,runlens)
    clens = cumsum(runlens);
    idx(clens(end))=0;
    idx([1 clens(1:end-1)+1]) = diff([0 vals]);
    out = cumsum(idx);
    return;

    标杆管理

    基准测试代码

    接下来列出的是基准测试代码，用于比较本帖子中所述的cumsum+diff方法与基于MATLAB 2014B的其他基于cumsum-only方法的运行时和加速。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    datasizes = [reshape(linspace(10,70,4).'*10.^(0:4),1,[]) 10^6 2*10^6]; %
    fcns = {'rld_cumsum','rld_cumsum_diff'}; % approaches to be benchmarked

    for k1 = 1:numel(datasizes)
        n = datasizes(k1); % Create random inputs
        vals = randi(200,1,n);
        runs = [5000 randi(200,1,n-1)]; % 5000 acts as an aberration
        for k2 = 1:numel(fcns) % Time approaches  
            tsec(k2,k1) = timeit(@() feval(fcns{k2}, vals,runs), 1);
        end
    end

    figure,      % Plot runtimes
    loglog(datasizes,tsec(1,:),'-bo'), hold on
    loglog(datasizes,tsec(2,:),'-k+')
    set(gca,'xgrid','on'),set(gca,'ygrid','on'),
    xlabel('Datasize ->'), ylabel('Runtimes (s)')
    legend(upper(strrep(fcns,'_',' '))),title('Runtime Plot')

    figure,      % Plot speedups
    semilogx(datasizes,tsec(1,:)./tsec(2,:),'-rx')        
    set(gca,'ygrid','on'), xlabel('Datasize ->')
    legend('Speedup(x) with cumsum+diff over cumsum-only'),title('Speedup Plot')

    rld_cumsum.m的相关功能代码：

    1
    2
    3
    4
    5
    function out = rld_cumsum(vals,runlens)
    index = zeros(1,sum(runlens));
    index([1 cumsum(runlens(1:end-1))+1]) = 1;
    out = vals(cumsum(index));
    return;

    运行时和加速图

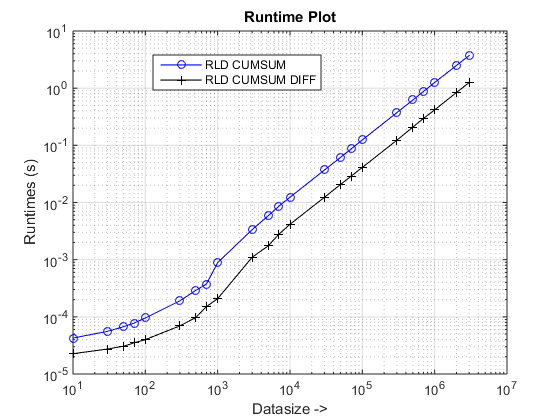
    enter image description here

    enter image description here

    结论

    与cumsum-only方法相比，建议的方法似乎使我们有了明显的提速，约为3倍！

    为什么这种基于cumsum+diff的新方法比以前的cumsum-only方法更好？

    好吧，原因的实质在于cumsum-only方法的最后一步，该方法需要将"累计"值映射到vals中。在新的基于cumsum+diff的方法中，我们正在做diff(vals)，而与sum(runLengths)元素数的映射相比，MATLAB只处理n元素(其中n是runLengths的数量)。 x27>方法，该数字必须是n的许多倍，因此，使用这种新方法的速度明显提高！

    相关讨论

    我没有内置函数，但这是一个解决方案：

    1
    2
    3
    index = zeros(1,sum(b));
    index([1 cumsum(b(1:end-1))+1]) = 1;
    c = a(cumsum(index));

    说明：

    首先创建一个零向量，其长度与输出数组的长度相同(即b中所有复制的总和)。然后将它们放在第一个元素中，每个随后的元素代表新值序列的开始将在输出中的位置。向量index的累积和然后可以用于索引到a，将每个值复制所需的次数。

    为了清楚起见，问题中给出的a和b的值的各种向量是这样的：

    1
    2
    3
            index = [1 0 1 0 1 1 0 0]
    cumsum(index) = [1 1 2 2 3 4 4 4]
                c = [1 1 3 3 2 5 5 5]

    编辑：为了完整起见，还有另一种使用ARRAYFUN的替代方法，但是，与上面的向量长达10,000个元素的解决方案相比，这似乎要花费20-100倍的时间来运行：

    1
    2
    c = arrayfun(@(x,y) x.*ones(1,y),a,b,'UniformOutput',false);
    c = [c{:}];
    相关讨论

    最终(自R2015a起)，有一个内置的文档功能，repelem。以下语法(其中第二个参数是向量)与此处相关：

    W = repelem(V,N), with vector V and vector N, creates a vector W where element V(i) is repeated N(i) times.

    换一种说法，" N的每个元素指定重复V的相应元素的次数"。

    例：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    >> a=[1,3,2,5]
    a =
         1     3     2     5
    >> b=[2,2,1,3]
    b =
         2     2     1     3
    >> repelem(a,b)
    ans =
         1     1     3     3     2     5     5     5

    从R2015b开始，MATLAB内置的repelem中的性能问题已得到修复。我已经运行了R2015b中chappjc帖子中的test_rld.m程序，并且repelem现在比其他算法快大约2倍：

    Updated plot comparing repelem execution time of different methods
    Speedup of repelem over cumsum+diff (about a factor 2)

    相关讨论